2 posts tagged with "neural networks"

"Even AI gotta practice clonin' Kendrick / The double entendre, the encore remnants." - Kendrick Lamar, America Has A Problem (Remix).

love all my supporters it’s time​

It’s been just over two weeks since Playboi Carti dropped his latest album. Since his last, we've seen more than four years of pushed-back dates, scrapped rollouts, and straight up lies. MUSIC is him thanking the world for the wait.

For those of you blissfully unaware of his existence, Playboi Carti is a rapper from Atlanta, a graduate of the SoundCloud rap scene, pioneer of the punk rap and rage sub-genres, and the definition of a dichotomous artist. Boundary-breaking or music-breaking? Depends on who you ask, but either way, it’s a bit strange for someone so known for his unparalleled creativity to be called out for using AI vocals. And, worse, this isn’t even the first time! But how did we get here?

D33pL34rning​

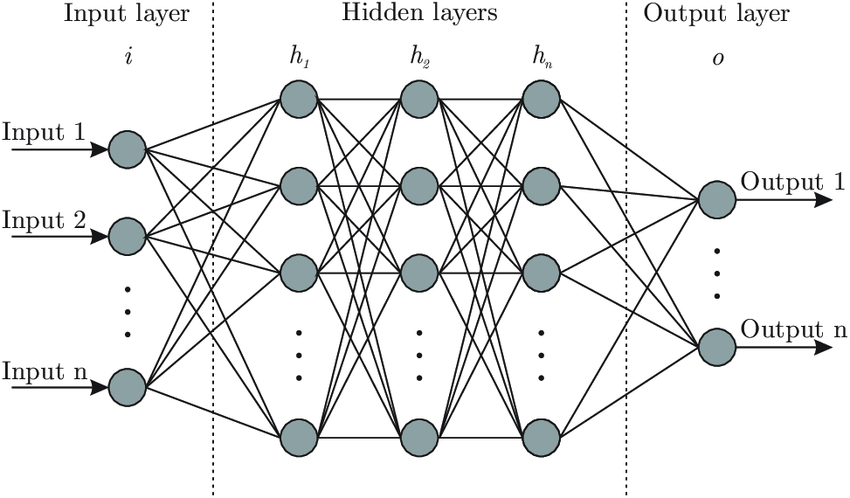
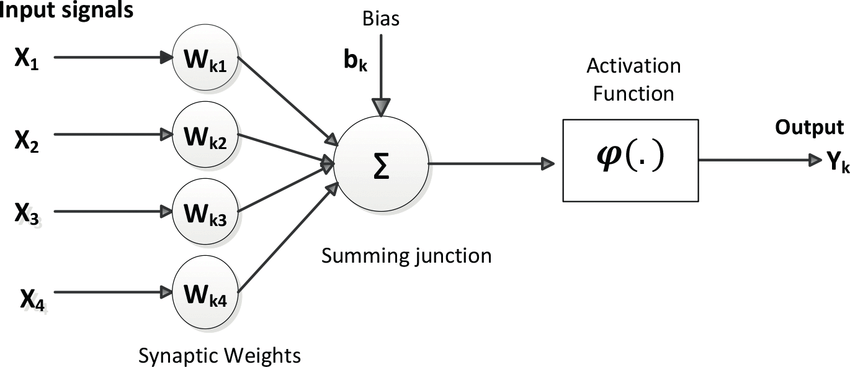
As with all AI worth worrying about, voice synthesis starts with a neural network. (And believe it or not, we have a brilliant article on neural networks here!) For most modern synthesisers, deep learning trains them on many hours of vocals by breaking down the speech into core pronunciations, to identify patterns and trends in speech. When the “voice” is output, it should replicate the intonations and flows of a human’s speech near-perfectly.

More advanced models, such as Meta’s Voicebox, use techniques such as non-deterministic mapping, which essentially allows for unlabelled variations to be fed as input, and implicit types and patterns in speech to be learnt from, instead of rigid homogenous maps. Voicebox itself can mimic a human voice with just two seconds of audio.

It wasn’t always this way. Voice synthesis, like early versions of Siri or an old sat-nav, was originally the arduous task of the respective algorithm chopping and splicing together thousands of lines of recorded human audio. Since then, it has improved exponentially. Today, a simple Google search and you can get Winston Churchill to sing “Espresso”.

No Auto?​

The claims are that Carti used an AI vocal overlay to morph his vocals into the flow and cadence of another musician, Lawson, on two tracks on MUSIC (“Rather Lie” and “Fine Shit”) and his feature on the Weeknd’s recent single “Timeless”. A video I could only find on the platform formerly known as Twitter presents “indisputable proof” of this, by comparing vocals which seemingly did not change at all between the (leaked) demo and release tracks.

Now, does this actually indisputably prove anything? Probably not. Do I care if he used AI on his own album? Well, this article wasn’t written to point fingers. I only care about the question of whether artistic integrity can be maintained when using AI, here in the context of music.

As with every new technology, one could argue it gives musicians the opportunities to further push creative boundaries. In 1997, Autotune was pitched as the answer to off-key singing. Jump forward 10 years and it’s the norm to disparage performances and the artists using it. But jump ahead another 10 years, and Autotune’s critics are yelling extremely out-of-tune with the current taste. Now, and back in 2017, autotune is everywhere. Modern pop would be unrecognisable without it. Plus, it spawned some brilliant new genres, such as hyperpop and melodic rap. Autotune is not a question of “yes” or “no” anymore, rather it’s “how much?”...

...though, this pivot could occur only after musical visionaries unlocked its potential for the world to appreciate. Think Daft Punk, T-Pain, Future, Charli XCX. Could this happen with AI? DJ David Guetta thinks so, and he describes it as just another “modern instrument” artists can now use to express a vision or feeling.

He is all but vindicated by the countless AI-generated tracks of artists performing lyrics they didn’t write or feel.

TUNDRA​

Another may argue that generative AI, as it remains, is ontologically destructive to creativity. While this view may seem alarmist, in the mainstream music sphere at least, AI vocals have only ever been used to imitate existing artists or older sounds, and not to cultivate a brand-new sound like with Autotune, or the synths, or drum machines, or samplers, before it. This is exactly why Carti’s new tracks sit in a grey area. It may be him, yet is it actually him if he’s using not just another rapper’s flow, but their voice too? Could it be a post-modern execution of songwriters using vocalists to express their vision?

Legally, the future looks challenging, if not bleak and barren. Musicians are taking muted protest. New amendments to UK government copyright laws would allow AI models to scrape internet content (including music) for training by default, unless the creator opts out. In response, over 1,000 musicians collaborated to release an album with no vocals or instruments just this February. Instead, you only the sounds and noises of everyday life.

Meanwhile, their record labels have moved fast, firing lawsuits and consistent lobbying for stricter artistic protection laws, but I do believe this speed is motivated by economics and not ethics. Find a method of using AI in music that is profitable for them and rest assured they will be the first to change their proverbial tune.

Further reading / references​

A. Downie and M. Hayes, “AI voice,” IBM, Jan. 23, 2025. https://www.ibm.com/think/topics/ai-voice

I. Parkel, “AI-generated song mimicking Drake and The Weeknd submitted for Grammy consideration,” The Independent, Sep. 07, 2023. https://www.independent.co.uk/arts-entertainment/music/news/drake-and-weeknd-ai-song-heart-on-my-sleeve-b2406902.html

L. Kuenssberg, “Sir Paul McCartney: Don’t let AI rip off musicians,” BBC News, Jan. 25, 2025. Available: https://www.bbc.co.uk/news/articles/c8xqv9g8442o

A. Owen, “Now and Then: The Use of AI on the ‘Final’ Beatles’ Song,” The Saint, Nov. 09, 2023. https://www.thesaint.scot/post/now-and-then-the-use-of-ai-on-the-final-beatles-song

Neural networks have shaped the way we interact with the world. From the deep learning technologies behind self-driving cars to the Natural Language Processing enhancements that power intelligent systems, neural networks are at the forefront of modern AI. But to truly appreciate the deep learning applications we use today, it’s important to examine the foundational theories that lay the groundwork for the field. By first looking at what a neural network is and then exploring the concepts underlying McCulloch and Pitts' theoretical neural network design, we can better appreciate the ingenuity of the technology that has transformed modern AI.

What is a Neural Network?​

A neural network is a computational model inspired by the structure of the brain. Neural networks typically consist of layers of nodes, or artificial neurons—an input layer, one or more hidden layers, and an output layer—connected to each other in a way that mimics the interconnected nature of neurons in the brain. Each node has its own weight and threshold associated with it. If the output of any individual node is above the specified threshold value, it becomes activated, passing information to the next layer. The network "learns" by adjusting the weights of these connections through a process called backpropagation, which minimizes errors over multiple training iterations.

Modern neural networks are complex multi-layered networks capable of solving intricate tasks like image recognition, natural language processing, and autonomous driving. They have had a profound impact on modern technology, revolutionizing and enriching people's lives through their application in solutions ranging from large language models like GPT-4 to advancements in healthcare, such as disease detection and drug discovery.

The Turing Machine​

To truly appreciate modern neural networks, it’s important to look at the story of their first theoretical inception. The origins of neural networks are intertwined with the origins of artificial intelligence itself, beginning in Cambridge in 1936, where a mathematician named Alan Turing was quietly laying the foundation for modern AI.

In 1936, Turing was tasked with the Entscheidungsproblem, a question posing whether there is an algorithm that can determine the truth or falsity of any statement within a specified system. To prove that no such algorithm exists for sufficiently complex systems, Turing invented a theoretical problem-solving machine called a Turing Machine. A Turing Machine consists of an infinite tape divided into cells, a head that can read and write symbols on the tape, and a set of rules. The machine operates by moving the head along the tape, reading symbols, and following the rules to write new symbols and move left or right, allowing it to simulate any algorithm given to it.

Using this, he answered the Entscheidungsproblem by proving that no algorithm can universally decide whether an arbitrary Turing machine will halt or run forever on a given input. This became known as the Halting Problem, which he detailed in his 1936 paper “On Computable Numbers, with an Application to the Entscheidungsproblem.” Turing’s insight—that any computable function could be broken down into simple operations through reading and writing symbols on an infinite tape—was a revolutionary idea that sparked the development of all artificial intelligence fields that followed.

The First Neural Network​

Inspired by Turing’s 1936 paper, Warren McCulloch, a neuroscientist, and Walter Pitts, a logician, published their influential 1943 paper "A Logical Calculus of the Ideas Immanent in Nervous Activity" in which they explored how the brain might perform computations. Turing’s paper provided a theoretical basis for thinking of computation in strictly formal terms and had shown that any computable function could be realized by a Turing machine. Pitts and McCulloch saw a parallel between Turing’s machine and the way groups of neurons might process and transmit information.

They proposed that neurons could be modeled as binary on-off units, firing when inputs exceeded a certain threshold (akin to receiving enough excitatory signals). By connecting these idealized neurons in various configurations, they demonstrated that the systems could implement basic logical operators like AND, OR, and NOT. This offered the possibility that these systems might simulate logical operations or even more complex computations. They were the first to describe what later researchers would call a neural network.

Although their model was only theoretical and faced several limitations, their mathematical approach to neural functioning inspired subsequent generations of researchers—paving the way for cybernetics and later the field of artificial intelligence. Their work ultimately shaped the path for modern AI and deep learning, which are now deeply embedded in our everyday lives.

References​

A. Turing, “On Computable Numbers, with an Application to the Entscheidungsproblem,” 1936. Available: https://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf.

W. S. Mcculloch and W. Pitts, “A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY*,” Bulletin of Mathematical Biology, vol. 52, no. 2, pp. 99–115, 1943, Available: https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McCulloch.and.Pitts.pdf.